| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 배열 예시
- mdn
- 트리 시간복잡도
- djangoprogramming
- djangoframework
- doubly linked list
- js입력받기
- singly linked list
- let const var 차이
- CLI 명령어
- django로그인
- 입력받기
- 배열 사례
- 맥북 터미널 명령어
- 시간복잡도
- 웹개발
- 웹프로그래밍
- 알고리즘
- 자바스크립트
- 배열이란
- 사용자입력
- linked list 현실 사례
- 리눅스 기초 명령어
- 장고
- python
- Django
- 자료구조
- js
- javascript
- let const 차이
- Today
- Total
용기러기's Coding World
알고리즘 시간 복잡도 (Algorithm Time Complexity) 본문
알고리즘 시간 복잡도에 대해서
알고는 있었지만,
이 키워드를 가지고 깊게 고민해본 적이 없는데
한번 짚고 넘어가야할 것 같아
정리를 해두고자 한다:D
먼저, 알고리즘 시간 복잡도에 대해서 나만의 정의를 해보면,
자료의 크기를 n이라고 했을 때,
이 n을 그래프의 가로축에 두고,
그 n이 점점 커진다고 했을 때
세로축에는 해당 자료를 가지고 수행하는 알고리즘의 걸리는 시간(time)이 오고,
이 때, 가로축과 세로축의 관계, 즉, 그래프의 선이 어떤 방향으로 가게 될지
반비례, 비례 관계 그리고 그 관계의 정도(기울기)를 시간 복잡도라고 생각해볼 수 있다.
마지막으로 간단 정리하면,
시간 복잡도는
자료크기가 커질 때,
그 자료를 바탕으로 수행하는 알고리즘의 수행 시간이
자료의 크기와 어떤 상관관계를 가지는지를 표현한 것이라고 볼 수 있다.
그리고 이는 Big O Notation(빅 오 노테이션)으로 표현할 수 있다.
예를 들어 살펴보면,
먼저,
O(1)의 시간 복잡도를 가지는
사례를 살펴보면,
특정한 배열에서 최대, 최소 값의 차를 구하는 것이 목표일 때
해당 배열이 이미 오름차순으로 정렬이 되어있는 상황을 가정해보자.
그러면, 결국 최대값은 배열의 맨 오른쪽에 있을 것이고, 최소값은 배열의 맨 왼쪽에 있을 것이다.
이 상황에서 최대-최소 값을 구하는 가장 효율적인 방법은
'배열[배열의 마지막 인덱스] - 배열[배열의 첫번째 인덱스]'를 해주는 것이다.
그런데, 이 때,
배열의 마지막 인덱스를 조회하고(1)
배열의 첫번째 인덱스를 조회하고(2)
그 둘을 빼는 시행을 하면(3)
결국 O(3)이 되어야 하는 것이 아닌가 생각할 수 있지만,
빅 오 노테이션은 과거에 수렴 개념을 생각해보면 이해하기 쉬운데
사실상 컴퓨터에게 1번의 수행과 3번의 수행은 별차이가 없다.
따라서, 상수는 모두 1로 표현하고,
n제곱 + n 일 때는 n제곱으로 표현한다.
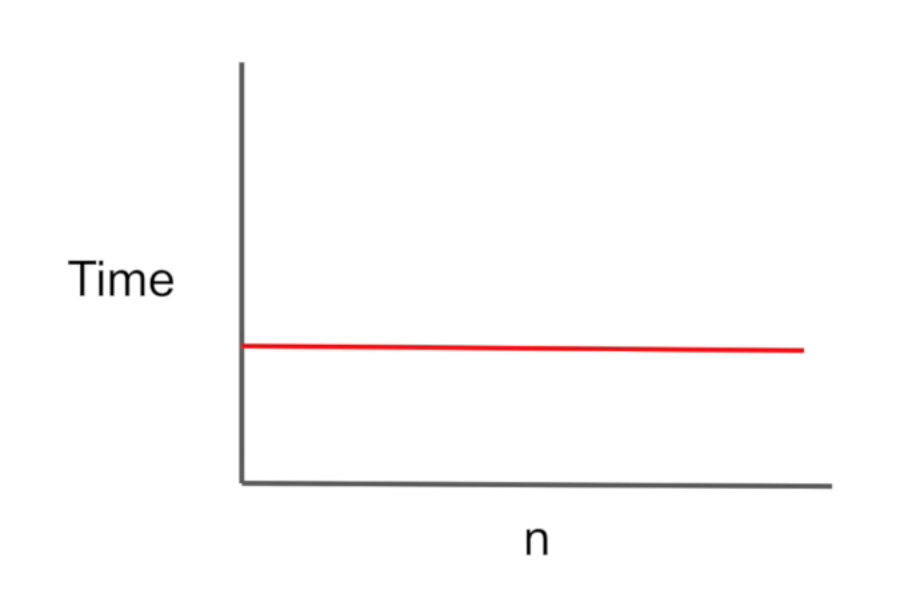
자료 출처 : 코드스테이츠
따라서, 위 경우의 시간 복잡도를 그래프로 표현해보면 위와 같아진다.
n이 아무리 증가해도 결국 걸리는 시간은 그대로인 것이다.
이는 시간 복잡도가 상대적으로 효율적이라는 것을 알 수 있다.
그렇다면, 자료의 크기의 증가와 걸리는 시간의 증가가 정비례 관계라면?
우리가 흔히 아는 기울기 1의 그래프가 될 것이다.
특이 케이스로 이진 탐색을 생각해보면
O(log n)이 되는데

자료 출처 : 코드스테이츠
위의 경우 기울기가 1과 유사하게 증가하다가
일정 자료 크기가 되면 평탄하게 증가하는 것을 볼 수 있다.
다음으로, 이중 for문을 쓸 때에 해당되는
O(n제곱), 즉, 자료의 크기가 증가함에 따라 시간은 그 자료크기의 제곱만큼 증가하는
알고리즘을 생각해볼 수 있다.

자료 출처 : 코드스테이츠
그럼, 마지막으로
어떻게보면.. 최악의 시나리오?
최악의 시간 복잡도를 가지는 알고리즘을 살펴보면,

자료 출처 : 코드스테이츠
이런식으로 자료의 크기가 커짐에 따라
기하급수적으로 시간이 늘어나는 유형이다.
O(cⁿ ) 의 시간복잡도를 가지는 이 유형은 자료의 크기의 제곱만큼 시간이 증가하는 이전 사례에 더하여
지수의 자료크기 제곱만큼의 속도로 시간이 증가하게 된다.

자료 출처 : 코드스테이츠
결과적으로, 여태까지 말한 사례를 장리해보면 이렇게 된다.
따라서, 알고리즘(문제 해결의 방법, 절차)을 설계할 때는
반드시 시간 복잡도를 생각해서 조금더 효율적인 알고리즘을
만들 수 있도록 노력해야겠다 :D
(알고리즘서 중요한 키워드 두개는 시간과 공간인데, 이 포스팅에서는 시간에만 초점을 맞췄다)
'용기러기's 알고리즘' 카테고리의 다른 글
| 자료 구조에 따른 시간 복잡도 비교 - linked list편 (0) | 2020.09.08 |
|---|---|
| 자료 구조에 따른 시간 복잡도 비교 - 배열편 (0) | 2020.09.08 |
| 알고리즘 일기 Day1 (0) | 2020.07.31 |



